Rechercher dans ce blog

Wednesday, January 3, 2024

Heat conductance of the quantum Hall bulk - Nature.com

Abstract

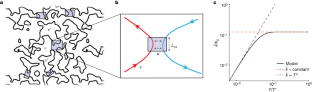
The quantum Hall effect is a prototypical realization of a topological state of matter. It emerges from a subtle interplay between topology, interactions and disorder1,2,3,4,5,6,7,8,9. The disorder enables the formation of localized states in the bulk that stabilize the quantum Hall states with respect to the magnetic field and carrier density3. Still, the details of the localized states and their contribution to transport remain beyond the reach of most experimental techniques10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31. Here we describe an extensive study of the bulk’s heat conductance. Using a novel ‘multiterminal’ short device (on a scale of 10 µm), we separate the longitudinal thermal conductance, \({\kappa }_{xx}T\) (owing to the bulk’s contribution), from the topological transverse value \({\kappa }_{xy}T\) by eliminating the contribution of the edge modes24. When the magnetic field is tuned away from the conductance plateau centre, the localized states in the bulk conduct heat efficiently (\({\kappa }_{xx}T\propto T\)), whereas the bulk remains electrically insulating. Fractional states in the first excited Landau level, such as the \(\nu =7/3\) and \(\nu =5/2\), conduct heat throughout the plateau with a finite \({\kappa }_{xx}T\). We propose a theoretical model that identifies the localized states as the cause of the finite heat conductance, agreeing qualitatively with our experimental findings.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Prices vary by article type

from$1.95

to$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Device and longitudinal thermal conductance at filling ν = 2.
Fig. 2: Temperature dependence of the longitudinal thermal conductance coefficient κxx at ν = 2.
Fig. 3: Illustration of the model used to calculate the bulk’s thermal conductance.
Fig. 4: Thermal conductance of the bulk at fillings ν = 7/3 and ν = 5/2.

Data availability

All relevant data have been provided in this paper. Additional information related to this work is available from the corresponding author upon reasonable request. Source data are provided with this paper.

References

  1. Laughlin, R. B. Quantized Hall conductivity in 2 dimensions. Phys. Rev. B 23, 5632–5633 (1981).

    Article  Google Scholar 

  2. Halperin, B. I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 25, 2185–2190 (1982).

    Article  Google Scholar 

  3. Prang, R. E. & Girvin, S. M. (eds) The Quantum Hall Effect (Springer, 1987).

  4. Tsui, D. C., Störmer, H. L. & Gossard, A. C. Zero-resistance state of two-dimensional electrons in a quantizing magnetic field. Phys. Rev. B 25, 1405–1407 (1982).

    Article  CAS  Google Scholar 

  5. Boebinger, G. S. et al. Activation energies and localization in the fractional quantum Hall effect. Phys. Rev. B 36, 7919–7929 (1987).

    Article  CAS  Google Scholar 

  6. Boebinger, G. S., Chang, A. M., Stormer, H. L. & Tsui, D. C. Magnetic field dependence of activation energies in the fractional quantum Hall effect. Phys. Rev. Lett. 55, 1606–1609 (1985).

    Article  CAS  PubMed  Google Scholar 

  7. Kane, C. L. & Fisher, M. P. A. Quantized thermal transport in the fractional quantum Hall effect. Phys. Rev. B 55, 15832–15837 (1997).

    Article  CAS  Google Scholar 

  8. Cappelli, A., Huerta, M. & Zemba, G. R. Thermal transport in chiral conformal theories and hierarchical quantum Hall states. Nucl. Phys. B 636, 568–582 (2002).

    Article  MathSciNet  Google Scholar 

  9. Read, N. & Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 61, 10267–10297 (2000).

    Article  CAS  Google Scholar 

  10. Jezouin, S. et al. Quantum limit of heat flow across a single electronic channel. Science 342, 601–604 (2013).

    Article  MathSciNet  CAS  PubMed  Google Scholar 

  11. Banerjee, M. et al. Observation of half-integer thermal Hall conductance. Nature 559, 205–210 (2018).

    Article  CAS  PubMed  Google Scholar 

  12. Banerjee, M. et al. Observed quantization of anyonic heat flow. Nature 545, 75–79 (2017).

    Article  CAS  PubMed  Google Scholar 

  13. Srivastav, S. K. et al. Universal quantized thermal conductance in graphene. Sci. Adv. 5, eaaw5798 (2019).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  14. Dutta, B., Umansky, V., Banerjee, M. & Heiblum, M. Isolated ballistic non-abelian interface channel. Science 377, 1198–1201 (2022).

    Article  CAS  PubMed  Google Scholar 

  15. Melcer, R. A. et al. Absent thermal equilibration on fractional quantum Hall edges over macroscopic scale. Nat. Commun. 13, 376 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  16. Srivastav, S. K. et al. Vanishing thermal equilibration for hole-conjugate fractional quantum Hall states in graphene. Phys. Rev. Lett. 126, 216803 (2021).

    Article  CAS  PubMed  Google Scholar 

  17. Srivastav, S. K. et al. Determination of topological edge quantum numbers of fractional quantum Hall phases by thermal conductance measurements. Nat. Commun. 13, 5185 (2022).

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  18. Altimiras, C. et al. Chargeless heat transport in the fractional quantum Hall regime. Phys. Rev. Lett. 109, 026803 (2012).

    Article  CAS  PubMed  Google Scholar 

  19. Venkatachalam, V., Hart, S., Pfeiffer, L., West, K. & Yacoby, A. Local thermometry of neutral modes on the quantum Hall edge. Nat. Phys. 8, 676–681 (2012).

    Article  CAS  Google Scholar 

  20. Inoue, H. et al. Proliferation of neutral modes in fractional quantum Hall states. Nat. Commun. 5, 4067 (2014).

    Article  CAS  PubMed  Google Scholar 

  21. Tanatar, M. A., Paglione, J., Petrovic, C. & Taillefer, L. Anisotropic violation of the Wiedemann–Franz law at a quantum critical point. Science 316, 1320–1322 (2007).

    Article  CAS  PubMed  Google Scholar 

  22. Wakeham, N. et al. Gross violation of the Wiedemann–Franz law in a quasi-one-dimensional conductor. Nat. Commun. 2, 396 (2011).

    Article  PubMed  Google Scholar 

  23. Crossno, J. et al. Observation of the Dirac fluid and the breakdown of the Wiedemann–Franz law in graphene. Science 351, 1058–1061 (2016).

    Article  CAS  PubMed  Google Scholar 

  24. Melcer, R. A., Konyzheva, S., Heiblum, M. & Umansky, V. Direct determination of the topological thermal conductance via local power measurement. Nat. Phys. 19, 327–332 (2023).

    Article  CAS  Google Scholar 

  25. Sammon, M., Banerjee, M. & Shklovskii, B. I. Giant violation of Wiedemann–Franz law in doping layers of modern AlGaAs heterostructures. Preprint at https://arxiv.org/abs/1904.04758 (2019).

  26. le Sueur, H. et al. Energy relaxation in the integer quantum Hall regime. Phys. Rev. Lett. 105, 056803 (2010).

    Article  PubMed  Google Scholar 

  27. Xia, J., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Evidence for a fractionally quantized Hall state with anisotropic longitudinal transport. Nat. Phys. 7, 845–848 (2011).

    Article  CAS  Google Scholar 

  28. Pan, W. et al. Exact quantization of the even-denominator fractional quantum Hall state at ν = 5/2 Landau level filling factor. Phys. Rev. Lett. 83, 3530–3533 (1999).

    Article  CAS  Google Scholar 

  29. Pan, W. et al. Experimental studies of the fractional quantum Hall effect in the first excited Landau level. Phys. Rev. B 77, 075307 (2008).

    Article  Google Scholar 

  30. Kumar, A., Csáthy, G. A., Manfra, M. J., Pfeiffer, L. N. & West, K. W. Nonconventional odd-denominator fractional quantum Hall states in the second Landau level. Phys. Rev. Lett. 105, 246808 (2010).

    Article  CAS  PubMed  Google Scholar 

  31. Rosenblatt, A. et al. Energy relaxation in edge modes in the quantum Hall effect. Phys. Rev. Lett. 125, 256803 (2020).

    Article  CAS  PubMed  Google Scholar 

  32. Lifshitz, E. M. & Pitaevskii, L. P. Physical Kinetics Vol. 10 (Elsevier Science, 1995).

  33. Oreg, Y. & Finkel’stein, A. M. Interedge interaction in the Quantum hall effect. Phys. Rev. Lett. 74, 3668–3671 (1995).

    Article  CAS  PubMed  Google Scholar 

  34. Gutman, D. B. et al. Energy transport in the Anderson insulator. Phys. Rev. B 93, 245427 (2016).

    Article  Google Scholar 

  35. Aita, H., Arrachea, L., Naón, C. & Fradkin, E. Heat transport through quantum Hall edge states: tunneling versus capacitive coupling to reservoirs. Phys. Rev. B 88, 085122 (2013).

    Article  Google Scholar 

  36. Balram, A. C., Jain, J. K. & Barkeshli, M. \(}_{n}\) superconductivity of composite bosons and the 7/3 fractional quantum Hall effect. Phys. Rev. Res. 2, 013349 (2020).

  37. Halperin, B. I. & Jain, J. K. Fractional Quantum Hall Effects (World Scientific, 2020).

  38. Ma, K. K. W., Peterson, M. R., Scarola, V. W. & Yang, K. Fractional quantum Hall effect at the filling factor ν = 5/2. Preprint at https://arxiv.org/abs/2208.07908 (2022).

  39. Son, D. T. Is the composite fermion a Dirac particle? Phys. Rev. 5, 031027 (2015).

    Article  Google Scholar 

  40. Zaletel, M. P., Mong, R. S. K., Pollmann, F. & Rezayi, E. H. Infinite density matrix renormalization group for multicomponent quantum Hall systems. Phys. Rev. B 91, 12 (2015).

    Article  Google Scholar 

  41. Rezayi, E. H. Landau level mixing and the ground state of the ν = 5/2 quantum Hall effect. Phys. Rev. Lett. 119, 026801 (2017).

    Article  PubMed  Google Scholar 

  42. Umansky, V. Y. et al. MBE growth of ultra-low disorder 2DEG with mobility exceeding 35 × 106 cm2/V S. J. Cryst. Growth 311, 1658–1661 (2009).

    Article  CAS  Google Scholar 

  43. Sivre, E. et al. Heat Coulomb blockade of one ballistic channel. Nat. Phys. 14, 145–148 (2018).

    Article  CAS  Google Scholar 

  44. Park, J., Mirlin, A. D., Rosenow, B. & Gefen, Y. Noise on complex quantum Hall edges: chiral anomaly and heat diffusion. Phys. Rev. B 99, 161302 (2019).

    Article  CAS  Google Scholar 

  45. Aharon-Steinberg, A., Oreg, Y. & Stern, A. Phenomenological theory of heat transport in the fractional quantum Hall effect. Phys. Rev. B 99, 041302 (2019).

    Article  CAS  Google Scholar 

  46. Johnson, J. B. Thermal agitation of electricity in conductors. Phys. Rev. 32, 97–109 (1928).

    Article  CAS  Google Scholar 

  47. Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev. 32, 110–113 (1928).

    Article  CAS  Google Scholar 

  48. Fukuyama, H. Two-dimensional wigner crystal under magnetic field. Solid State Commun. 17, 1323–1326 (1975).

    Article  Google Scholar 

  49. Maciejko, J., Hsu, B., Kivelson, S. A., Park, Y. & Sondhi, S. L. Field theory of the quantum Hall nematic transition. Phys. Rev. B 88, 125137 (2013).

    Article  Google Scholar 

Download references

Acknowledgements

We thank A. D. Mirlin for fruitful discussions. A.G. and E.B. acknowledge support from the Israel Science Foundation (Quantum Science and Technology Grant 2074/19) and the Deutsche Forschungsgemeinschaft (Grant CRC 183). M.H. acknowledges support from the European Research Council (the European Union’s Horizon 2020 Research and Innovation Program Grant 833078). A.S. acknowledges support from the Israel Science Foundation (Quantum Science and Technology Grant 2074/19), the Deutsche Forschungsgemeinschaft (Grant CRC 183 and Project C02) and the European Research Council (the European Union’s Horizon 2020 Research and Innovation Program Grants 788715 and 817799 and Project LEGOTOP).

Author information

Authors and Affiliations

  1. Braun Center for Submicron Research, Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot, Israel

    Ron Aharon Melcer, Arup Kumar Paul, Priya Tiwari, Vladimir Umansky & Moty Heiblum

  2. Department of Condensed Matter Physics, Weizmann Institute of Science, Rehovot, Israel

    Ron Aharon Melcer, Avigail Gil, Arup Kumar Paul, Priya Tiwari, Vladimir Umansky, Moty Heiblum, Yuval Oreg, Ady Stern & Erez Berg

Authors
  1. Ron Aharon Melcer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Avigail Gil
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Arup Kumar Paul
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Priya Tiwari
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Vladimir Umansky
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Moty Heiblum
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Yuval Oreg
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Ady Stern
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Erez Berg
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

R.A.M. designed the experiment, fabricated the devices, performed the measurements and analysed the data. R.A.M., A.K.P. and P.T. performed length dependence measurements. M.H. supervised the experiment’s design, execution and data analysis. A.G., Y.O., A.S. and E.B. developed the theoretical model. V.U. grew the GaAs heterostructures. All authors contributed to the writing of the manuscript.

Corresponding author

Correspondence to Moty Heiblum.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Francois Parmentier, Bo Yang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Methodology of power measurement.

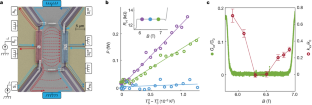
Measurement and analysis steps required to measure the heat flow and extract \({\kappa }_}\). As an example, we present \(\nu =2\) data, measured at \(B=6.1{\rm{T}}\), and base temperature of \({T}_{0}=15{\rm{mK}}\). (a) Raw noise data. The excess noise measured at \({A}_}\) and \({A}_}\) as a function of the sourced current \(I\) sourced from \({S}_{1}\) (while current \(-I\) is simultaneously sourced from \({S}_{2}\)). (b) Power-metre’s temperature as a function of the source’s temperature extracted from (a) using Eq. M7. The heating of the source from \({T}_{0}=15{\rm{mk}}\) to a temperature \({T}_} \sim 40{\rm{mK}}\) causes the slight increase of the PM’s temperature \({T}_} \sim 17{\rm{mK}}\), due to the finite \({\kappa }_}\). (c) Power-metre calibration; raw data. Noise measured at \({A}_}\) as a function of the direct heating of the PM, by current \({I}_}\) sourced from \({S}_{1}^}\) (while current \(-{I}_}\) is simultaneously sourced from \({S}_{2}^}\)). (d) Dissipated power (derived from Eq. M9) as a function of \({T}_}\). (e) By combining the main measurement (b) with the calibration (d), we can plot the power arriving to the PM as a function of the source temperature, and produce the plot presented in the main text Fig. 2a. A linear fit to the power vs. \({T}_}^{2}\) gives \({\kappa }_}\).

Extended Data Fig. 2 κxx for different device distance.

The dissipated power in the PM as a function of the source’s temperature squared, for two different PM-to-source-distances (measured in different devices), \(10\,\mu m\) and 20 \(\mu m.\) For both fractional states \(\nu =5/2\) (a) and \(\nu =7/3\) (b). We observe a decrease of the transferred heat with S-PM distance. This corresponds to \({\kappa }_}\) reducing from \({\kappa }_}=0.37\pm 0.03{\kappa }_{0}\) (\({\kappa }_}=0.24\pm 0.01{\kappa }_{0}\)) at \(10\,\mu m\) to \({\kappa }_}=0.17\pm 0.02{\kappa }_{0}\) (\({\kappa }_}=0.15\pm 0.01{\kappa }_{0}\)) at \(20\,\mu m\) for \(\nu =\frac{5}{2}\)(\(\nu =7/3\)). Data measured at the plateau centre at \({T}_{0}=10{\rm{mK}}\).

Extended Data Fig. 3 ‘Two terminal’ thermal conductance on the ν = 2 plateau, at T0 = 15mK.

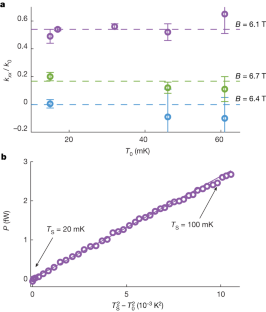
(a) Power dissipated at the source, \({P}_}\), as a function of the source’s temperature squared, for different magnetic fields on the \(\nu =2\) plateau. The low temperature data (up to \(27{\rm{mK}}\)) is linearly fitted to extract the two-terminal thermal conductance, \({\kappa }_{2{\rm{T}}}\), which changes mildly with magnetic field. (b) Top-panel -\({\kappa }_{2{\rm{T}}}\), extracted from (a) as a function of the magnetic field (includes 2k0 due to donors), with an increase away from plateau centre due to the short bulk. Bottom-panel - \({\kappa }_}\), and \({G}_}\) as a function of the magnetic field (identical to Fig. 2b). It appears that the appearance of finite heat conductance through the bulk causes \({\kappa }_{2{\rm{T}}}\) to increase slightly.

Extended Data Fig. 4 Thermal conductance through the bulk of other QHE states.

Longitudinal electrical conductance (green with scale to the left) and longitudinal thermal conductance (red markers with scale on the right) plotted as a function of magnetic field on the plateaus of (a) \(\nu =3\), (b) \(\nu =4/3\) and (c) \(\nu =2\). The circular markers corresponds to the fitting results of \(P\) vs. \({T}_}^{2}\) (raw data presented in Extended Data Fig. 5), and the triangular markers correspond to \({\kappa }_}\) measured for a single source temperature of \({T}_}=50{\rm{mK}}\), and extracted according to Eq. M11.

Extended Data Fig. 5 Raw data used to extract κxx.

The coloured markers represent the power arriving to the PM as a function of the source temperature squared. The data is linearly fitted (coloured straight lines) to extract \({\kappa }_}\) (according to Eq. 1 of the main text). Showing the measured data for the results appearing in the main text and the supplementary information: (a) \(\nu =2\), (b) \(\nu =7/3\), (c), \(\nu =5/2\) and \(\nu =8/3\), (d) \(\nu =3\) and (e) \(\nu =4/3\).

Extended Data Fig. 6 Amplifier calibration.

Equilibrium noise as a function of the cryostat temperature (markers). The noise is linear in temperature, in agreement with the Johnson-Nyquist formula (Eq. M13). This allows us to calibrate the gain according to Eq. M14 (straight lines).

Supplementary information

Source data

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Melcer, R.A., Gil, A., Paul, A.K. et al. Heat conductance of the quantum Hall bulk. Nature (2024). https://ift.tt/ohTx5LQ

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://ift.tt/ohTx5LQ

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Adblock test (Why?)


Heat conductance of the quantum Hall bulk - Nature.com
Read More
at
Labels:

No comments:

Post a Comment

Subscribe to: Post Comments (Atom)

Dear Lina, – The Brooklyn Rail - Brooklyn Rail

Goethe’s “To Lina” commands that the letters of the page, black on white, be not read but breathed so that our hearts “now can break.” What...